Casa
strangers to friends

Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers

Por um escritor misterioso

Descrição
Let’s take a look at Alice first. To her, each one of the other five (Bob, Carol, Dave, Ellen, and Frank) is either a friend or a stranger. Suppose Bob, Dave, and Frank are friends to Alice, and…
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Solved Counting: product rule, sum rule, inclusion-exclusion
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
How to prove: at a party of six people either there are three mutual acquaintances or there are three mutual strangers - Quora
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Madeline Dawsey--Modular Forms and Ramsey Theory.
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Proof by cases example: Three mutual friends/enemies theorem
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Ramsey Theory on Facebook - Scientific American Blog Network
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
SOLVED: Prove this theorem: Among any six people, there exists a group of 3 mutual friends or a group of 3 mutual strangers. (Here friends and strangers are considered symmetric relations, i.e.
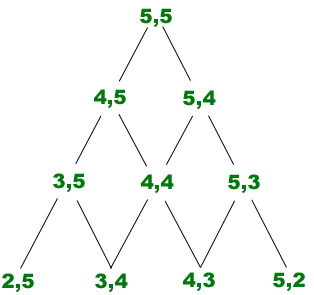
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friends and strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friends and strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Ramsey's Theorem: Friends and Strangers
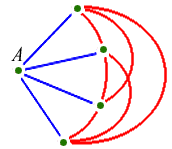
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friends and strangers
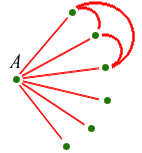
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friends and strangers
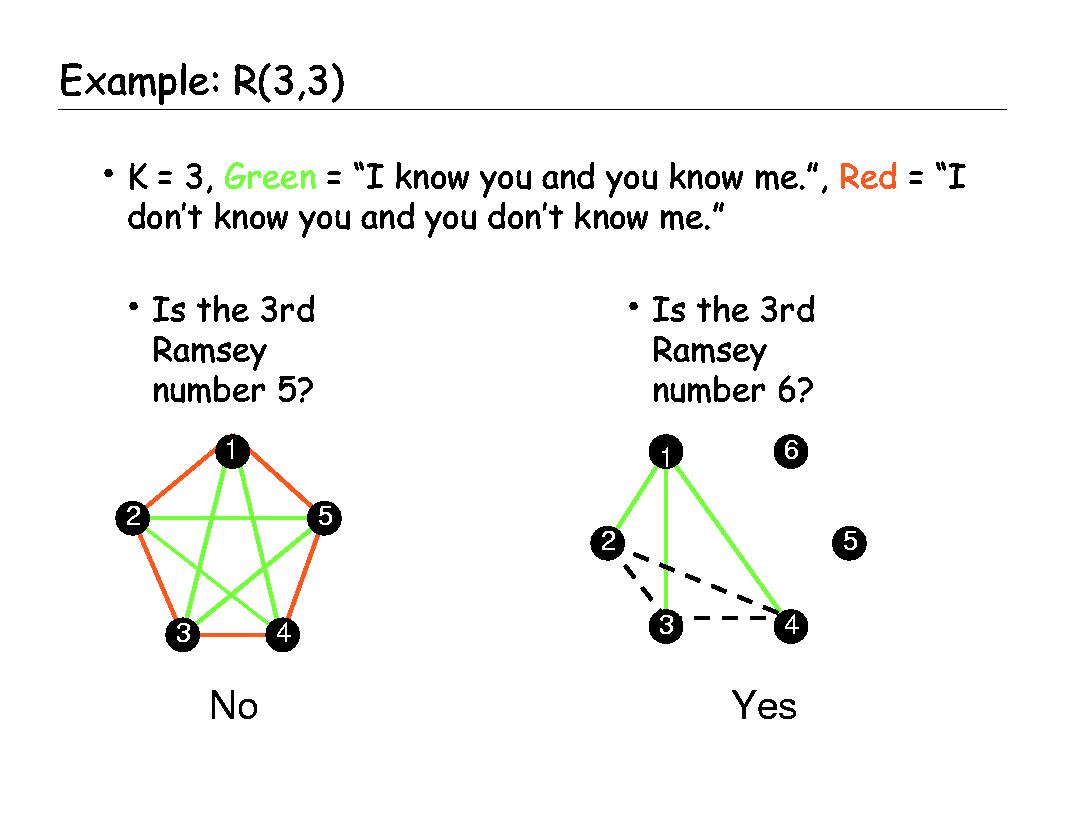
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
CS290I Lecture notes -- Let's Party
de por adulto (o preço varia de acordo com o tamanho do grupo)